Chỉ báo Linear Regression là một kỹ thuật thống kê được sử dụng để phân tích mối quan hệ giữa hai biến. Nó cho phép dự đoán giá trị của một biến phụ thuộc (được gọi là biến phản hồi) dựa trên giá trị của một hoặc nhiều biến độc lập (được gọi là biến đầu vào).
Trong Linear Regression, chúng ta giả định rằng có một mối quan hệ tuyến tính giữa biến phản hồi và các biến đầu vào. Mục tiêu của Linear Regression là tìm ra một đường thẳng tốt nhất để mô tả mối quan hệ này.
Để đánh giá mức độ phù hợp của mô hình Linear Regression, chúng ta sử dụng các chỉ báo như R-squared, F-statistic và các giá trị t-test để kiểm tra tính đáng tin cậy của các hệ số mô hình.
Thông tin chi tiết về chỉ báo Linear Regression:
Chỉ báo Linear Regression là một kỹ thuật thống kê được sử dụng để xây dựng một mô hình dự đoán giá trị của một biến phụ thuộc (được gọi là biến phản hồi) dựa trên giá trị của một hoặc nhiều biến độc lập (được gọi là biến đầu vào). Trong mô hình Linear Regression, giả định rằng có một mối quan hệ tuyến tính giữa biến phản hồi và các biến đầu vào.
Chỉ báo Linear Regression bao gồm các hệ số như hệ số góc (slope) và hệ số chặn (intercept) của đường hồi quy (regression line) để mô tả mối quan hệ tuyến tính giữa biến phản hồi và biến đầu vào. Hệ số góc đại diện cho sự thay đổi của biến phản hồi đối với mỗi đơn vị thay đổi của biến đầu vào, trong khi hệ số chặn đại diện cho giá trị của biến phản hồi khi tất cả các biến đầu vào đều bằng 0.
Một số chỉ báo Linear Regression phổ biến:
- R-squared (R²): Chỉ số R-squared là một phương tiện để đánh giá mức độ phù hợp của mô hình Linear Regression. Nó đo lường tỷ lệ phương sai của biến phụ thuộc được giải thích bởi mô hình so với tổng phương sai của biến phụ thuộc. R-squared có giá trị nằm trong khoảng từ 0 đến 1, và giá trị càng gần 1 thì mô hình càng phù hợp.
- Giá trị F (F-statistic): Giá trị F được sử dụng để kiểm tra tính đáng tin cậy của mô hình Linear Regression. Giá trị F cao có nghĩa là mô hình Linear Regression phù hợp hơn, vì nó chỉ ra rằng hệ số góc khác không đáng kể.
- Giá trị t-test: Giá trị t-test được sử dụng để kiểm tra tính đáng tin cậy của từng hệ số của mô hình Linear Regression. Giá trị t-test cao có nghĩa là hệ số tương ứng với biến đầu vào đó đáng tin cậy.
Lưu ý:
- Đảm bảo các giả định của Linear Regression được tuân thủ: Mô hình Linear Regression đòi hỏi các giả định về phân phối, độ đo và các điều kiện khác được tuân thủ. Cần kiểm tra các giả định này để đảm bảo kết quả của mô hình đáng tin cậy.
- Kiểm tra tính đáng tin cậy của mô hình: Cần kiểm tra tính đáng tin cậy của mô hình Linear Regression bằng cách sử dụng các chỉ báo như R-squared, F-statistic và các giá trị t-test để đảm bảo rằng các hệ số mô hình đáng tin cậy và mô hình phù hợp.
- Kiểm tra các điểm ngoại lai (outliers) và giá trị bất thường (anomalies): Các điểm ngoại lai và giá trị bất thường có thể ảnh hưởng đến mô hình Linear Regression và dẫn đến kết quả sai lệch. Cần kiểm tra và xử lý các điểm ngoại lai và giá trị bất thường này trước khi xây dựng mô hình.
- Xác định mối quan hệ tuyến tính giữa các biến: Mô hình Linear Regression giả định rằng có một mối quan hệ tuyến tính giữa biến phụ thuộc và các biến đầu vào. Nếu không có mối quan hệ tuyến tính, mô hình Linear Regression sẽ không phù hợp.
- Sử dụng mô hình Linear Regression cẩn thận: Mô hình Linear Regression có thể được sử dụng để dự đoán giá trị của biến phụ thuộc dựa trên các biến đầu vào, tuy nhiên, cần sử dụng cẩn thận và cân nhắc kỹ trước khi sử dụng mô hình để tránh các sai lầm trong dự đoán và đưa ra quyết định sai lệch.
Mô tả:
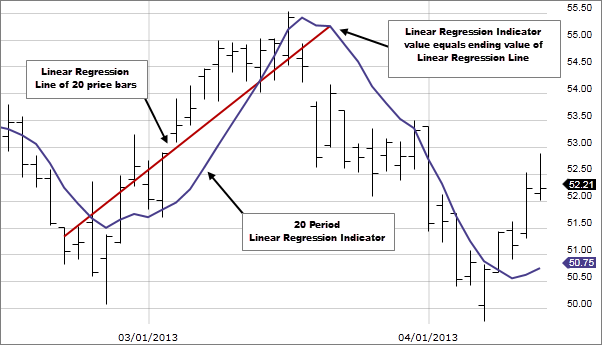
Chỉ báo Linear Regression (Hồi quy tuyến tính) trình bày giá trị kết thúc của đường hồi quy tuyến tính trong một số thanh xác định; cho thấy về mặt thống kê, giá được dự kiến sẽ ở đâu. Ví dụ, Chỉ báo Linear Regression với chu kỳ 20 sẽ bằng giá trị kết thúc của đường hồi quy tuyến tính trên 20 thanh.
Cách thức hoạt động của chỉ báo này
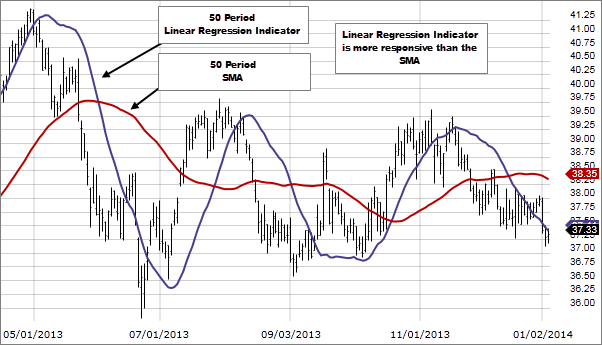
Cách diễn giải của Chỉ báo Linear Regression tương tự như đường trung bình động (moving average) nhưng nó có một lợi thế so với đường trung bình động. Thay vì vẽ đường trung bình của hành động giá trong quá khứ, nó vẽ đường hồi quy tuyến tính nơi mà mong đợi giá sẽ đến, làm cho Chỉ báo Linear Regression đáp ứng nhanh hơn so với đường trung bình động.
Cách tính chỉ báo
Mỗi điểm trong chỉ báo Linear Regression chỉ đơn giản là điểm cuối của một đường xu hướng Linear Regression với chu kỳ n.
Để tính chỉ báo Linear Regression, trước hết cần xác định số thanh dùng để tính toán. Sau đó, ta sẽ tính toán giá trung bình của các giá đó để tạo thành một đường Linear Regression. Sau đó, chỉ báo sẽ trình bày giá trị kết thúc của đường Linear Regression này trên mỗi thanh thời gian.
Công thức tính Linear Regression Indicator như sau:
- Xác định số thanh để tính toán (ví dụ: 20).
- Tính toán giá trung bình của các giá đó trong 20 thanh để tạo thành một đường Linear Regression.
- Tính giá trị của đường Linear Regression tại cuối mỗi thanh thời gian và vẽ nó lên đồ thị.
Chú ý: Việc tính toán Linear Regression có thể được thực hiện bằng tay hoặc bằng phần mềm máy tính hoặc các công cụ phân tích kỹ thuật khác.
Ứng dụng chỉ báo Linear Regression
Chỉ báo Linear Regression có nhiều ứng dụng trong phân tích kỹ thuật và giao dịch trên thị trường tài chính, ví dụ như:
- Xác định xu hướng thị trường: giúp nhà đầu tư xác định xu hướng của thị trường bằng cách theo dõi đường Linear Regression. Nếu đường này đang tăng, có thể xem đó là tín hiệu của một xu hướng tăng.
- Điểm vào và ra khỏi thị trường: Nhà đầu tư có thể sử dụng Chỉ báo Linear Regression để xác định điểm vào và ra khỏi thị trường. Khi đường Linear Regression đang tăng, có thể mua vào. Ngược lại, khi đường Linear Regression đang giảm, có thể bán ra.
- Xác định điểm mua và bán chính xác hơn: Chỉ báo giúp nhà đầu tư xác định điểm mua và bán chính xác hơn bằng cách theo dõi đường Linear Regression và các điểm chéo giữa giá và đường Linear Regression.
- Quản lý rủi ro: Nó cũng có thể được sử dụng để quản lý rủi ro trong giao dịch bằng cách đặt các stop-loss order dựa trên mức độ gần hoặc xa so với đường Linear Regression.
Kết luận:
Trong kỹ thuật giao dịch trên thị trường tài chính, Chỉ báo Linear Regression là một công cụ quan trọng để xác định xu hướng thị trường và điểm mua bán chính xác. Với khả năng phản ứng nhanh hơn so với các chỉ báo khác như Moving Average, Linear Regression Indicator có thể giúp nhà đầu tư tối ưu hóa lợi nhuận và quản lý rủi ro hiệu quả.
Tuy nhiên, như với bất kỳ công cụ phân tích kỹ thuật nào khác, Chỉ báo Linear Regression không phải là công cụ hoàn hảo và có thể mang lại kết quả không chính xác trong một số trường hợp. Do đó, nhà đầu tư cần phải sử dụng nó kết hợp với các công cụ phân tích kỹ thuật khác và đánh giá sự phù hợp của nó với chiến lược giao dịch của mình trước khi quyết định sử dụng.
Tham gia giao dịch cùng Saigontradecoin tại đây!
Đường link các sàn:
- Binance: Link đăng ký tài khoản Binance
- Huobi: Link đăng ký tài khoản Huobi
- Kucoin: Link đăng ký tài khoản Kucoin
- MEXC: Link đăng ký tài khoản MEXC
- OKX: Link đăng ký tài khoản OKX
- Bybit: Link đăng ký tài khoản Bybit
- Gate.io: Link đăng ký tài khoản Gate.io
- BingX: Link đăng ký tài khoản BingX

